Задача 1. Основания BC и AD трапеции равны соответственно 5 и 20, BD = 10. Докажите, что треугольники CBD и ADB подобны.
ДОКАЗАТЕЛЬСТВО
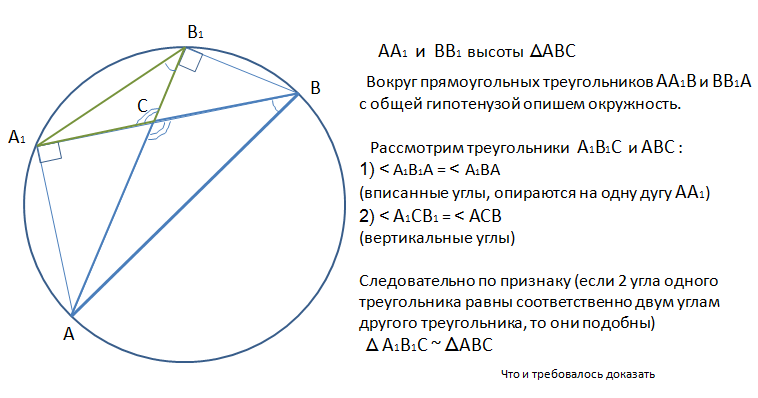
Задача 2. В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1B1C и ABC подобны.
ДОКАЗАТЕЛЬСТВО
1 способ:

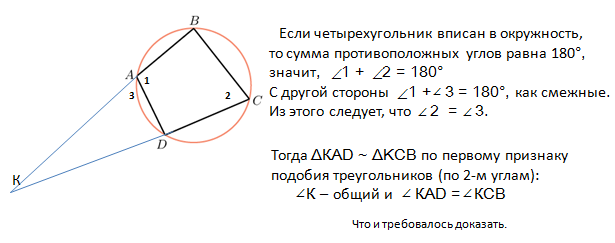
Задача 3. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон CD и AB четырёхугольника пересекаются в точке K. Докажите, что треугольники KAD и KCB подобны.
ДОКАЗАТЕЛЬСТВО
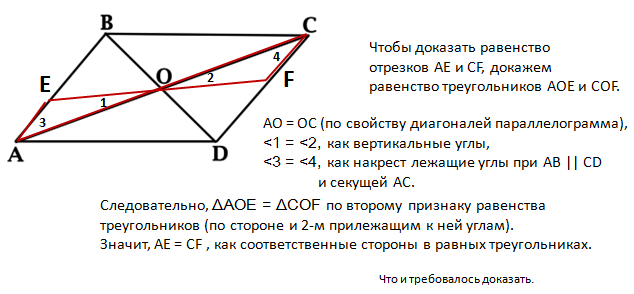
Задача 4. Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках E и F соответственно. Докажите, что отрезки AE и CF равны.
ДОКАЗАТЕЛЬСТВО
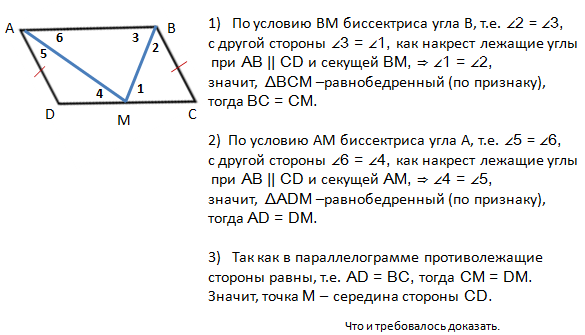
Задача 5. Сторона AD параллелограмма ABCD вдвое больше стороны CD. Точка M – середина стороны AD. Докажите, что CM – биссектриса угла BCD.
ДОКАЗАТЕЛЬСТВО

Задача 6. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке M, лежащей на стороне CD. Докажите, что M – середина CD.
ДОКАЗАТЕЛЬСТВО
Задача 7. Биссектрисы углов A и D трапеции ABCD пересекаются в точке M, лежащей на стороне BC. Докажите, что точка M равноудалена от прямых AB, AD и CD.
ДОКАЗАТЕЛЬСТВО

Задача 8. Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
ДОКАЗАТЕЛЬСТВО
