Задача 1. Основание АС равнобедренного треугольника АВС равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания АС в его середине. Найдите радиус окружности, вписанной в треугольник АВС.
РЕШЕНИЕ

Задача 2. Основание АС равнобедренного треугольника АВС равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания АС в его середине. Найдите радиус окружности, вписанной в треугольник АВС.
РЕШЕНИЕ

Задача 3. В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
РЕШЕНИЕ

Задача 4. В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 8 и 6. Найдите площадь параллелограмма ABCD.
РЕШЕНИЕ

Задача 5. В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 14, BC = 12.
РЕШЕНИЕ

Задача 6. В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 15, BC = 14.
РЕШЕНИЕ

Задача 7. В выпуклом четырехугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырехугольника NPQM можно описать окружность, PQ = 14, SQ = 4.
РЕШЕНИЕ

Задача 8. В выпуклом четырехугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырехугольника NPQM можно описать окружность, PQ = 86, SQ = 43.
РЕШЕНИЕ

Задача 9. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 96, тангенс угла BAC равен 8/15. Найдите радиус окружности, вписанной в треугольник ABC.
РЕШЕНИЕ

Задача 10. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник АCP, равен 4, тангенс угла BAC равен 3/4. Найдите радиус окружности, вписанной в треугольник ABC.
РЕШЕНИЕ

Задача 11. На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC = 40, BC = 34 и CD = 20.
РЕШЕНИЕ

Задача 12. На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC = 38, BC = 34 и CD = 19.
РЕШЕНИЕ

Задача 13. Диагонали четырехугольника ABCD, вершины которого расположены на окружности, пересекаются в точке M. Известно, что ∠ABC = 72° , ∠BCD = 102° , ∠AMD = 110° . Найдите ∠ACD.
РЕШЕНИЕ

Задача 14. Диагонали четырехугольника ABCD, вершины которого расположены на окружности, пересекаются в точке M. Известно, что ∠ABC = 74° , ∠BCD = 102° , ∠AMD = 112° . Найдите ∠ACD.
РЕШЕНИЕ

Задача 15. Длина катета AC прямоугольного треугольника ABC равна 8. Окружность с диаметром AC пересекает гипотенузу AB в точке M. Найдите площадь треугольника ABC, если известно, что AM: MB = 16 : 9.
РЕШЕНИЕ

Задача 16. Длина катета AC прямоугольного треугольника ABC равна 3. Окружность с диаметром AC пересекает гипотенузу AB в точке M. Найдите площадь треугольника ABC, если известно, что AM: MB = 9 : 16.
РЕШЕНИЕ

Задача 17. На каждой из двух окружностей с радиусами 3 и 4 лежат по три вершины ромба. Найдите его сторону.
РЕШЕНИЕ

Задача 18. На каждой из двух окружностей с радиусами 2,5 и 6 лежат по три вершины ромба. Найдите его сторону.
РЕШЕНИЕ

Задача 19. Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в ее середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
РЕШЕНИЕ

Задача 20. Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в ее середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
РЕШЕНИЕ

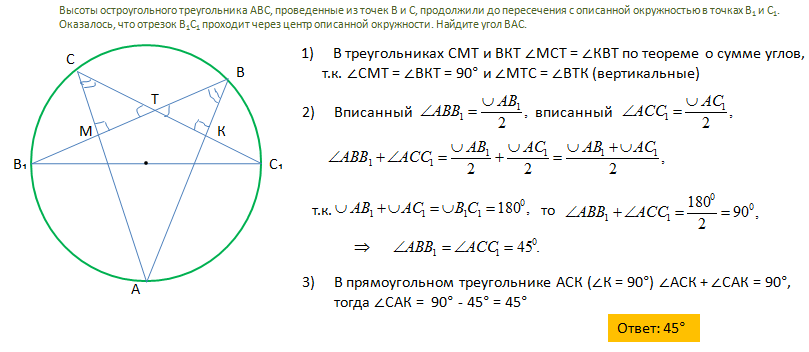
Задача 21. Высоты остроугольного треугольника ABC, проведенные из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
РЕШЕНИЕ