Сообщество учителей Горкуновой Ольги

Круглые тела

Задача 1. Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?

ПРОВЕРЬ ОТВЕТ

2,25

Задача 2. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?

ПРОВЕРЬ ОТВЕТ

Задача 3. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?

ПРОВЕРЬ ОТВЕТ

Задача 4. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.

ПРОВЕРЬ ОТВЕТ

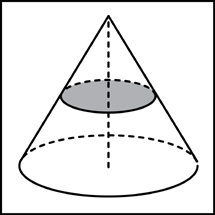
Задача 5. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

ПРОВЕРЬ ОТВЕТ

Задача 6. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?

ПРОВЕРЬ ОТВЕТ

Задача 7. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.

ПРОВЕРЬ ОТВЕТ

Задача 8. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на п .

ПРОВЕРЬ ОТВЕТ

128

Задача 9. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.

ПРОВЕРЬ ОТВЕТ

Задача 10. Во сколько раз уменьшится площадь боковой поверхности конуса, если его радиус его основания уменьшить в 1,5 раза?

ПРОВЕРЬ ОТВЕТ

1,5

Задача 11. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на п .

ПРОВЕРЬ ОТВЕТ

128

Задача 12. Найдите объем конуса, площадь основания которого равна 2, а образующая равна 6 и наклонена к плоскости основания под углом 30^circ.

ПРОВЕРЬ ОТВЕТ

Задача 13. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.

ПРОВЕРЬ ОТВЕТ

Задача 14. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/п.

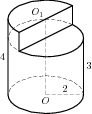
ПРОВЕРЬ ОТВЕТ

Задача 15. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на П.

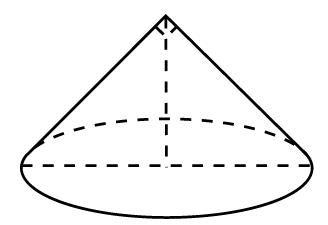
ПРОВЕРЬ ОТВЕТ

Задача 16. В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ дайте в сантиметрах.

ПРОВЕРЬ ОТВЕТ

Задача 17. Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1: 2 , считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?

ПРОВЕРЬ ОТВЕТ

Задача 18. Во сколько раз уменьшится объём конуса, если его высота уменьшится в 9 раз, а радиус основания останется прежним?

ПРОВЕРЬ ОТВЕТ

1. Свой блок открываем