Суббота, 27.07.2024, 11:33
Приветствую Вас Гость
Задача 1. Окружности радиусов 60 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
РЕШЕНИЕ

Задача 2. Окружности радиусов 22 и 99 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
РЕШЕНИЕ

Задача 3. Две касающиеся внешним образом в точке K окружности, радиусы которых равны 16 и 48, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
РЕШЕНИЕ

Задача 4. Две касающиеся внешним образом в точке K окружности, радиусы которых равны 36 и 45, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
РЕШЕНИЕ

Задача 5. Три окружности с центрами А, В и С и радиусами 2,5, 0,5 и 4,5 соответственно попарно касаются внешним образом. Найдите угол АВС.
РЕШЕНИЕ

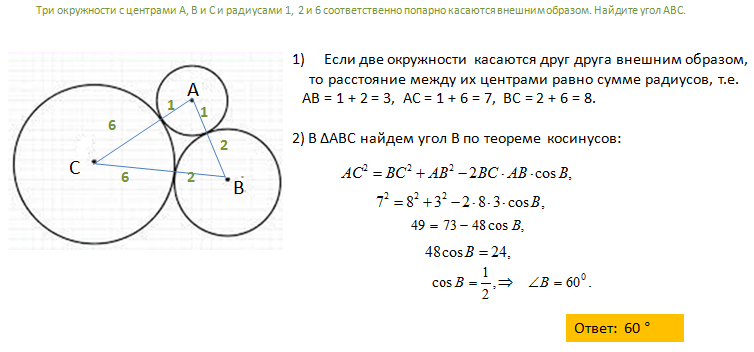
Задача 6. Три окружности с центрами А, В и С и радиусами 1, 2 и 6 соответственно попарно касаются внешним образом. Найдите угол АВС.
РЕШЕНИЕ
Задача 7. Две окружности с центрами А и С и радиусами 4,5 и 2,5 касаются друг с другом внешним образом и внутренним образом касаются окружности с центром В радиусом 7,5. Найдите угол АВС.
РЕШЕНИЕ

Задача 8. Две окружности с центрами А и С и радиусами 7 и 6 касаются друг с другом внешним образом и внутренним образом касаются окружности с центром В радиусом 14. Найдите угол АВС.
РЕШЕНИЕ

Задача 9. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трех окружностей.
РЕШЕНИЕ

Задача 10. Три окружности, радиусы которых равны 2, 4 и 6, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трех окружностей.
РЕШЕНИЕ

Задача 11. Окружность радиуса 4 касается внешним образом второй окружности в точке В. Общая касательная к этим окружностям, проходящая через точку В, пересекается с некоторой другой их общей касательной в точке А. Найдите радиус второй окружности, если АВ = 6 .
РЕШЕНИЕ

Задача 12. Окружность радиуса 2 касается внешним образом второй окружности в точке В. Общая касательная к этим окружностям, проходящая через точку В, пересекается с некоторой другой их общей касательной в точке А. Найдите радиус второй окружности, если АВ = 4 .
РЕШЕНИЕ

Задача 13. В окружности с центром в точке О проведены две хорды АВ и СD. Прямые АВ и СD перпендикулярны и пересекаются в точке М, лежащей вне окружности. При этом АМ = 36, ВМ = 6, CD = 4√46 . Найдите OM.
РЕШЕНИЕ

Задача 14. В окружности с центром в точке О проведены две хорды АВ и СD. Прямые АВ и СD перпендикулярны и пересекаются в точке М, лежащей вне окружности. При этом АМ = 17, ВМ = 3, CD = 10√21. Найдите OM.
РЕШЕНИЕ

Задача 15. В прямоугольном треугольнике ABC с прямым углом B, проведена биссектриса угла A. Известно, что она пересекает серединный перпендикуляр, проведенный к стороне BC в точке K. Найдите угол BCK, если известно, что угол ACB равен 40°.
РЕШЕНИЕ

Задача 16. В прямоугольном треугольнике ABC с прямым углом B, проведена биссектриса угла A. Известно, что она пересекает серединный перпендикуляр, проведенный к стороне BC в точке K. Найдите угол BCK, если известно, что угол ACB равен 20°.
РЕШЕНИЕ

| Вход на сайт |
| Калькулятор |
| Формулы |
| Площадь треугольника
Основные формулы тригонометрии Производные основных функций Линейная функция |
| Поиск |
| Календарь |
| Архив записей |
| Наш опрос |
| Мини-чат |
| Статистика |
| Друзья сайта |