Это важно знать!
Задание 1. Заполните таблицу, вписав соответствующие элементы подобных треугольников:
| Соответствующие вершины | Соответственно равные углы | Сходственные стороны | |||
| 1) |  |
проверь
Ответ: А и А1 B и B1 C и C1 |
проверь
Ответ: ∠А и ∠А1 ∠B и ∠B1 ∠C и ∠C1 |
проверь
Ответ: AB и А1B1 BC и B1C1 AC и А1C1 |
|
| 2) |  |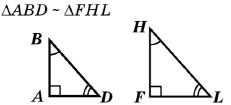
проверь
Ответ: А и F B и H D и L |
проверь
Ответ: ∠А и ∠F ∠B и ∠H ∠D и ∠L |
проверь
Ответ: АB и FH BD и HL AD и FL |
|
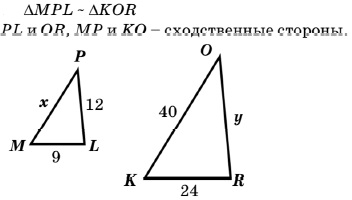
| 3) |  |
проверь
Ответ: N и R M и P K и O |
проверь
Ответ: ∠N и ∠R ∠M и ∠P ∠K и ∠O |
проверь
Ответ: NM и RP MK и PO NK и RO |
|
| 4) |  |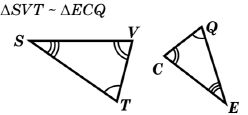
проверь
Ответ: T и Q V и C S и E |
проверь
Ответ: ∠T и ∠Q ∠V и ∠C ∠S и ∠E |
проверь
Ответ: TV и QC VS и CE TS и QE |
|
Задание 2. Заполните таблицу:
| Соответствующие вершины | Сходственные стороны | Пропорциональность сходственных сторон | |||
| 1) |
проверь
Ответ: K и O M и P N и R |
проверь
Ответ: KM и OP MN и PR KN и OR |
проверь
Ответ: |
||
| 2) |
проверь
Ответ: D и L H и T F и U |
проверь
Ответ: DH и LT HF и TU DF и LU |
проверь
Ответ: |
||
| 3) |
проверь
Ответ: A и C B и D K и L |
проверь
Ответ: AB и CD BK и DL AK и CL |
проверь
Ответ: |
||
| 4) |
проверь
Ответ: P и F Q и D R и C |
проверь
Ответ: PQ и FD QR и DC PR и FC |
проверь
Ответ: |
||
Задание 3. Найдите неизвестные стороны х и у подобных треугольников:
1) 
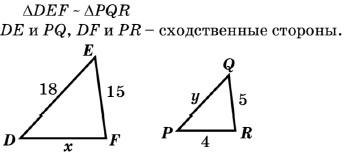проверьОтвет: x = 12, y = 62) проверьОтвет: x = 35, y = 183) проверьОтвет: x = 15, y = 324) проверьОтвет: x = 31,25, y = 11,2
Задание 4. Зная, что 
, заполните таблицу:
Задание 5. Зная, что, заполните таблицу:
Задание 6. Вставьте пропущенное слово/слова:
Задание 7. Определите, верно ли утверждение:
1. Свой блок открываем
| Сходственные стороны | |||||
| AB | MK | ||||
| 1) | 5 | 3 |
проверь
Ответ: |
проверь
Ответ: |
проверь
Ответ: |
| 2) | 10 | 7 |
проверь
Ответ: |
проверь
Ответ: |
проверь
Ответ: |
| 3) | 9 | 12 |
проверь
Ответ: |
проверь
Ответ: |
проверь
Ответ: |
| 4) | 5 | 30 |
проверь
Ответ: |
проверь
Ответ: |
проверь
Ответ: |
| 5) | 16 | 10 |
проверь
Ответ: |
проверь
Ответ: |
проверь
Ответ: |
Задание 5. Зная, что
| Сходственные стороны | |||||||
| AB | MK | ||||||
| 1) | 8 | 4 |
проверь
Ответ: 2 |
18 |
проверь
Ответ: 9 |
12 |
проверь
Ответ: 3 |
| 2) | 5 | 15 |
проверь
Ответ: |
16 |
проверь
Ответ: 48 |
12 |
проверь
Ответ: 108 |
| 3) | 3 | 9 |
проверь
Ответ: |
проверь
Ответ: 12 |
36 |
проверь
Ответ: 4 |
36 |
| 4) |
проверь
Ответ: 6 |
3 | 2 |
проверь
Ответ: 108 |
54 |
проверь
Ответ: 144 |
36 |
| 5) | 4 |
проверь
Ответ: |
3 | 12 |
проверь
Ответ: 4 |
6 |
проверь
Ответ: |
| 6) | 13 |
проверь
Ответ: 26 |
проверь
Ответ: |
32 | 64 | 24 |
проверь
Ответ: 96 |
| 7) | 15 |
проверь
Ответ: 25 |
проверь
Ответ: |
36 | 60 | 54 |
проверь
Ответ: 150 |
| 8) |
проверь
Ответ: 5 |
20 |
проверь
Ответ: |
проверь
Ответ: 12 |
48 | 6 | 96 |
| 9) | 12 |
проверь
Ответ: 4 |
3 | 54 |
проверь
Ответ: 18 |
90 |
проверь
Ответ: 10 |
| 10) | 7 | 21 |
проверь
Ответ: |
проверь
Ответ: 16 |
48 |
проверь
Ответ: |
84 |
Задание 6. Вставьте пропущенное слово/слова:
1) Отношением отрезков АВ и CD называется отношение их ... .
проверь
Ответ: длин
2) Два треугольника называются подобными, если их углы соответственно ... и стороны одного треугольника ... сходственным сторонам другого.
проверь
Ответ: равны, пропорциональны
3) Число k, равное отношению сходственных сторон подобных треугольников, называется ... .
проверь
Ответ: коэффициентом подобия
4) Отношение периметров двух подобных треугольников равно ... .
проверь
Ответ: коэффициенту подобия
5) Отношение площадей двух подобных треугольников равно ... коэффициента подобия.
проверь
Ответ: квадрату
6) Отношение линейных элементов двух подобных треугольников равно ... подобия.
проверь
Ответ: коэффициенту
Задание 7. Определите, верно ли утверждение:
1) Равносторонний и прямоугольный треугольники могут быть подобными.
проверь
Ответ: нет
2) Равнобедренный и прямоугольный треугольники могут быть подобными.
проверь
Ответ:да
3) В любых двух подобных треугольниках три пары равных углов.
проверь
Ответ: да
4) Если два треугольника подобны, то сходственные стороны равны.
проверь
Ответ: нет
5) Если основания подобных равнобедренных треугольников относятся 1 : 3, то площади этих треугольников относятся как 1 : 9.
проверь
Ответ: да